Page 76 - 4234
P. 76
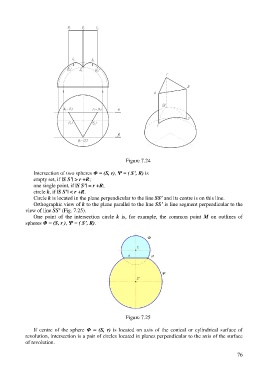
Figure 7.24
Intersection of two spheres Φ = (S, r), Ψ = ( S’, R) is
empty set, if |S S’| > r +R;
one single point, if |S S’| = r +R;
circle k, if |S S’| < r +R.
Circle k is located in the plane perpendicular to the line SS’ and its centre is on this line.
Orthographic view of k to the plane parallel to the line SS’ is line segment perpendicular to the
view of line SS’ (Fig. 7.25).
One point of the intersection circle k is, for example, the common point M on outlines of
spheres Φ = (S, r ), Ψ = ( S’, R).
Figure 7.25
If centre of the sphere Φ = (S, r) is located on axis of the conical or cylindrical surface of
revolution, intersection is a pair of circles located in planes perpendicular to the axis of the surface
of revolution.
76