Page 53 - 4234

The sum of the number of faces and vertices is two more then the number of edges in the
solids above. This result was proved by the Swiss mathematician Leonhard Euler (1707 - 1783).
Euler’s Theorem: The number of faces (F), vertices (V), and edges (E) of a polyhedron are
related by the formula:

F + V = E + 2.

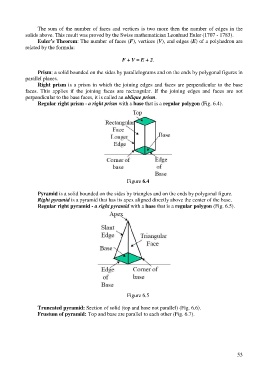
Prism: a solid bounded on the sides by parallelograms and on the ends by polygonal figures in
parallel planes.
Right prism is a prism in which the joining edges and faces are perpendicular to the base
faces. This applies if the joining faces are rectangular. If the joining edges and faces are not
perpendicular to the base faces, it is called an oblique prism.
Regular right prism - a right prism with a base that is a regular polygon (Fig. 6.4).

Figure 6.4

Pyramid is a solid bounded on the sides by triangles and on the ends by polygonal figure.
Right pyramid is a pyramid that has its apex aligned directly above the center of the base.
Regular right pyramid - a right pyramid with a base that is a regular polygon (Fig. 6.5).

Figure 6.5

Truncated pyramid: Section of solid (top and base not parallel) (Fig. 6.6).
Frustum of pyramid: Top and base are parallel to each other (Fig. 6.7).

53