Page 20 - 4206

1
2
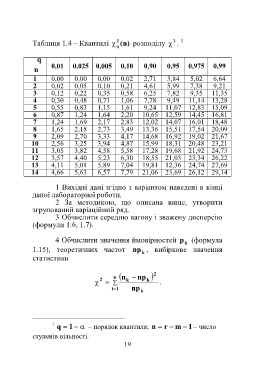
Таблиця 1.4 – Квантилі  2 q ) n ( розподілу  .

q
0,01 0,025 0,005 0,10 0,90 0,95 0,975 0,99
n
1 0,00 0,00 0,00 0,02 2,71 3,84 5,02 6,64
2 0,02 0,05 0,10 0,21 4,61 5,99 7,38 9,21
3 0,12 0,22 0,35 0,58 6,25 7,82 9,35 11,35
4 0,30 0,48 0,71 1,06 7,78 9,49 11,14 13,28
5 0,55 0,83 1,15 1,61 9,24 11,07 12,83 15,09
6 0,87 1,24 1,64 2,20 10,65 12,59 14,45 16,81
7 1,24 1,69 2,17 2,83 12,02 14,07 16,01 18,48
8 1,65 2,18 2,73 3,49 13,36 15,51 17,54 20,09
9 2,09 2,70 3,33 4,17 14,68 16,92 19,02 21,67
10 2,56 3,25 3,94 4,87 15,99 18,31 20,48 23,21
11 3,05 3,82 4,58 5,58 17,28 19,68 21,92 24,73
12 3,57 4,40 5,23 6,30 18,55 21,03 23,34 26,22
13 4,11 5,01 5,89 7,04 19,81 12,36 24,74 27,69
14 4,66 5,63 6,57 7,79 21,06 23,69 26,12 29,14

1 Вихідні дані згідно з варіантом наведені в кінці
даної лабораторної роботи.
2 За методикою, що описана вище, утворити
згрупований варіаційний ряд.
3 Обчислити середню вагову і зважену дисперсію
(формули 1.6, 1.7).

4 Обчислити значення ймовірностей p (формула
k
1.15), теоретичних частот np , вибіркове значення
k
статистики

к n  np  2
 2   k k .
i 1 np k

1
 1q   – порядок квантиля; n  r  m  1 – число
ступенів вільності.
19