Page 44 - 4167

m 1 m 2
F  G 2 . . (4.2)
r
In vector form
 m  m 
F 12   G 1 2 r  12 , (4.3)
r 3 12

where r is radius-vector from the particle to the second one. Really the
12
very same force acts on the second particle, but in opposite direction
 
F 21   F .
12
G is gravitation constant which numerical value depends on the

units in which force, mass, and length are expressed. Apparently,
gravitation constant is numerical equal of force of gravitational
attraction between two particles of mass m  m  1 kg on distance m1
2
1
between them According to modern experiments gravitation constant
is equal to

 11 N  m 2
G  , 6 ( 67390 10  , 0 0001 ) .
kg 2

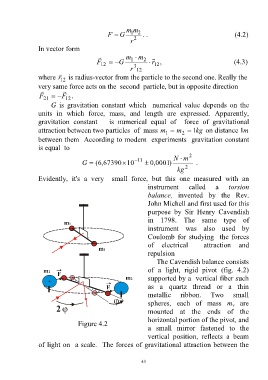
Evidently, it's a very small force, but this one measured with an
instrument called a torsion
balance, invented by the Rev.

John Michell and first used for this
purpose by Sir Henry Cavendish
in 1798. The same type of
instrument was also used by

Coulomb for studying the forces
of electrical attraction and
repulsion

The Cavendish balance consists
of a light, rigid pivot (fig. 4.2)
supported by a vertical fiber such

as a quartz thread or a thin
metallic ribbon. Two small
spheres, each of mass m are
v
mounted at the ends of the
horizontal portion of the pivot, and
Figure 4.2
a small mirror fastened to the
vertical position, reflects a beam

of light on a scale. The forces of gravitational attraction between the

43