Page 17 - 4167

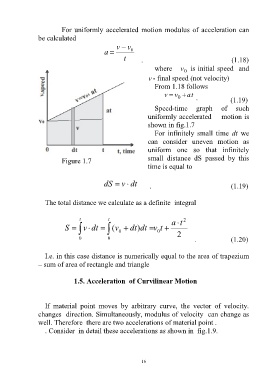
For uniformly accelerated motion modulus of acceleration can
be calculated
v  v 0
a 
t . (1.18)

where v is initial speed and
0
v - final speed (not velocity)
From 1.18 follows

v  v  t a . (1.19)
0
Speed-time graph of such

uniformly accelerated motion is
shown in fig.1.7
For infinitely small time dt we
can consider uneven motion as

uniform one so that infinitely
small distance dS passed by this
Figure 1.7
time is equal to

dS  v  dt . (1.19)

The total distance we calculate as a definite integral

t t 2
a t
S  v dt  ( v 0  dt) dt  tv 0 


0 0 2 . (1.20)

I.e. in this case distance is numerically equal to the area of trapezium
– sum of area of rectangle and triangle

1.5. Acceleration of Curvilinear Motion

If material point moves by arbitrary curve, the vector of velocity.
changes direction. Simultaneously, modulus of velocity can change as
well. Therefore there are two accelerations of material point .

. Consider in detail these accelerations as shown in fig.1.9.

16