Page 100 - 2589

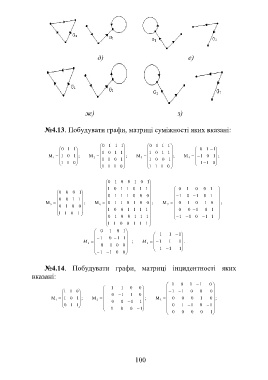
д) е)

ж) з)

№4.13. Побудувати графи, матриці суміжності яких вказані:

0  1 1 1 0  1 1 1 
0  1 1      0 1  1
  1  0 1 1  1  0 1 1   
M  1  0 1 ;  M  ; M  ; M    1 0 1 ; 
1 2  1 1 0 1  3  1 0 0 1  4
 1 1 0       1 1 0 
       
 1 1 1 0   1 1 1 0 

0  1 0 0 1 0 1
 
1  0 1 1 0 1 1   0 1 0 0 1 
0  0 0 1  
   0 1 1 1 0 0 0    1 0  1 0 1 
 0 0 1 1     
M    ; M  0  1 1 0 1 0 0 ; M   0 1 0 1 0  ;
7
5
6
 0 1 0 0   1 0 0 1 1 1 1   0 0  1 0 1 
   
 1 1 0 1   
0  1 0 0 1 1 1    1  1 0  1 1 
 
 1 1 0 0 1 1 1 
 0 1 0 1
   1 1  1 
  1 0  1 1  
M  ; M    1 1 1 . 
8  0 1 0 0  9
   1  1 1 
   
  1  1 0 0 

№4.14. Побудувати графи, матриці інцидентності яких
вказані:
 1 0 1  1 0 
  1 1 0 0   
1  1 0     1  1 0 0 0 
   0  1 1 0 
M  1  0 1 ;  M  ; M   0 0 0 1 0  ;
1 2  0 0  1 1  3  
 0 1 1    0 1  1 0 
     1 
 1 0 0  1   
 0 0 0 0 1 

100