Page 28 - 21

Визначаємо реакції балки. Для цього розглянемо рівновагу балки OAB ек-
вівалентної системи під дією зовнішнього навантаження і знайденого опорного

моменту X (рис. 3.2).
1
 M B  ;0 R  6  X  q 4  5 ; 0 R  72, 7 кн.
A
1
A
Розглянемо рівновагу балки CD (рис. 3.2).
 M C  ;0  R  5  F 2  X  ; 0 R D  4, 602 кн.
2
D
З рівнянь рівноваги визначимо реакції R і R .
B C
R  88, 523 кн; R  106, 182 кн.
B C
Для проведення деформаційної перевірки знаходяться переміщення пере-

різу балки у будь-якій з її опор (дивись п. 3.3).

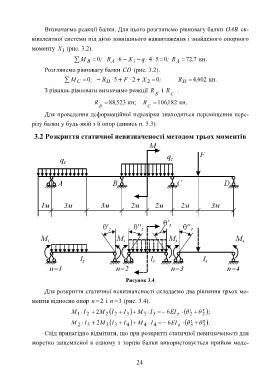
3.2 Розкриття статичної невизначеності методом трьох моментів

Рисунок 3.4

Для розкриття статичної невизначеності складаємо два рівняння трьох мо-

ментів відносно опор n 2 і n 3 (рис. 3.4).


M 1 I 2  2M 2 I 2  I 3  M 3 I 3   6EI z     2    ;
2

M 2  I 3  2M 3 I 3  I 4  M 4 I 4   6EI z     3    .
3
Слід принагідно відмітити, що при розкритті статичної невизначеності для
жорстко защемленої в одному з торців балки використовується прийом моде-

24