Page 101 - 128

спектру росте, і номер останньої з них, величина якої більше
1% амплітуди немодульованого коливання несучої частоти,
визначається по наближеній формулі
k=1+m+m. (6.33)
Ця формула дає позитивні результати для найбільш
поширених значень m (0,5  m  24). У випадку, коли 
ширина спектра близька до величини 2, коли >>
ширина спектра близька до величини 2.

J o

100

80

60

40 2.4048 8.6537 14.9308

0

-40 5.5201 11.7915 18.0711 m
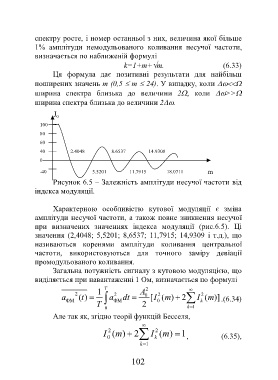
Рисунок 6.5 – Залежність амплітуди несучої частоти від
індекса модуляції.

Характерною особливістю кутової модуляції є зміна
амплітуди несучої частоти, а також повне зникнення несучої
при визначених значеннях індекса модуляції (рис.6.5). Ці
значення (2,4048; 5,5201; 8,6537; 11,7915; 14,9309 і т.д.), що
називаються коренями амплітуди коливання центральної
частоти, використовуються для точного заміру девіації
промодульованого коливання.
Загальна потужність сигналу з кутовою модуляцією, що
виділяється при навантаженні 1 Ом, визначається по формулі
T 2 
1 A
2 2 0 2 2
a  t) (   a  dt  [ I ( m)  2  k m)] .(6.34)
I (
0
T 2
0 k 1
Але так як, згідно теорії функцій Бесселя,

I 0 2 (m )  2  k 2 (m ) 1 , (6.35),
I
k 1
102