Page 220 - 6251

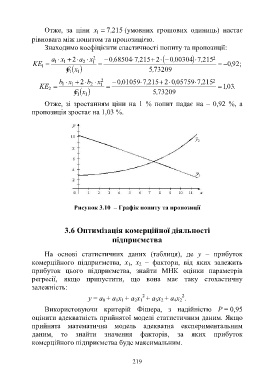
Отже, за ціни x  7, 215 (умовних грошових одиниць) настає

1

рівновага між попитом та пропозицією.
Знаходимо коефіцієнти еластичності попиту та пропозиції:

a  x  2 a  x 2  0, 68504 7, 215 2  0, 00304  7, 215 2
KE  1 1 2 1    0, 92;
1
y € 1  x 1 5, 73209

b  x  2 b  x  2  0 ,01059 7 ,215 2 0  ,05759 7 ,215 2
KE  1 1 2 1   1 ,03 .
2
y € 1  x 1 5 ,73209

Отже, зі зростанням ціни на 1 % попит падає на – 0,92 %, а
пропозиція зростає на 1,03 %.

Рисунок 3.10 – Графік попиту та пропозиції

3.6 Оптимізація комерційної діяльності

підприємства

На основі статистичних даних (таблиця), де у – прибуток
комерційного підприємства, х , х – фактори, від яких залежить
1
2
прибуток цього підприємства, знайти МНК оцінки параметрів
регресії, якщо припустити, що вона має таку стохастичну

залежність:
2 2
у = а + а х + а х + а х + а х .
3 2
2 1
1 1
0
4 2
Використовуючи критерій Фішера, з надійністю Р = 0,95
оцінити адекватність прийнятої моделі статистичним даним. Якщо
прийнята математична модель адекватна експериментальним
даним, то знайти значення факторів, за яких прибуток
комерційного підприємства буде максимальним.

219