Page 24 - 6028

проектування фільтра. Однак ці проблеми зазвичай невеликі, а 513 - хороша довжина для
більшості застосувань.
Крім необхідної величини масиву, показаної в (a), повинен бути відповідний
фазовий масив тієї ж довжини. У цьому прикладі фаза необхідного частотного відгуку
повністю дорівнює нулю (цей масив не показаний на малюнку 17-1). Як і в разі масиву
амплітуд, фазовий масив може бути будь-якою довільною кривою. Однак пам'ятайте, що
перший і останній відлік (тобто, 0 і 512) фазової матриці повинні мати значення 0 (або
кратне 2π, що є одним і тим же). Частотна характеристика також може бути задана в
прямокутній формі, визначаючи записи масиву для реальної та уявної частин замість
використання амплітуди і фази.

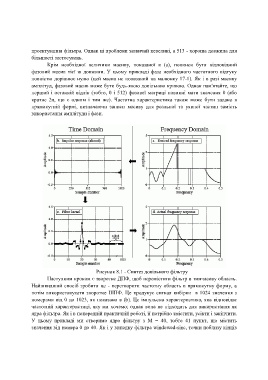
Рисунок 8.1 - Синтез довільного фільтру
Наступним кроком є зворотне ДПФ, щоб перемістити фільтр в тимчасову область.
Найшвидший спосіб зробити це - перетворити частотну область в прямокутну форму, а
потім використовувати зворотне ШПФ. Це продукує сигнал вибірки в 1024 значення з
номерами від 0 до 1023, як показано в (b). Це імпульсна характеристика, яка відповідає
частотній характеристиці, яку ми хочемо; однак вона не підходить для використання як
ядра фільтра. Як і в попередній практичній роботі, її потрібно змістити, усікти і закінчити.
У цьому прикладі ми створимо ядро фільтру з M = 40, тобто 41 пункт, що містить
значення від номера 0 до 40. Як і у випадку фільтра windowed-sinc, точки поблизу кінців