Page 53 - 5

*
*
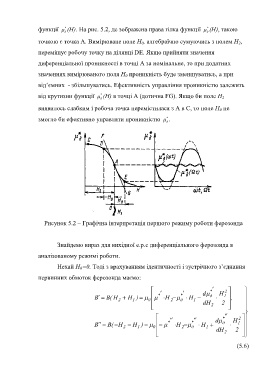
функції  (Н). На рис. 5.2, де зображена права гілка функції  (Н), такою
д д
точкою є точка А. Вимірюване поле Н 0, алгебраїчно сумуючись з полем Н 2,

переміщує робочу точку на ділянці DE. Якщо прийняти значення

диференціальної проникності в точці А за номінальне, то при додатних

значеннях вимірюваного поля Н 0 проникність буде зменшуватись, а при

від’ємних - збільшуватись. Ефективність управління проникністю залежить

*
від крутизни функції  (Н) в точці А (дотична FG). Якщо би поле Н 2
д
виявилось слабким і робоча точка перемістилася з А в С, то поле Н 0 не

змогло би ефективно управляти проникністю  .
*
д

Рисунок 5.2 – Графічна інтерпретація першого режиму роботи ферозонда

Знайдемо вираз для вихідної е.р.с диференціального ферозонда в

аналізованому режимі роботи.

Нехай Н 0=0. Тоді з врахуванням ідентичності і зустрічного з’єднання

первинних обмоток ферозонда маємо:

   d *  H 2  
  B ( B H 2  H 1 )   0   * H 2  *  H 1  д  1  , 
д
 dH 2  
 2  

   *  2  
   B ( B H  H )      * H  *  H  d д  H 1  
2
1
0
 2 д 1 dH 2  
 2  
(5.6)