Page 20 - 4824

U 3

6

L

3

U 1
▼R(u) 3 6

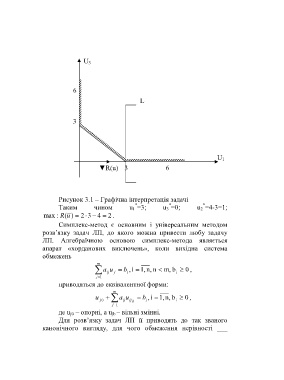
Рисунок 3.1 – Графічна інтерпретація задачі
* * *
Таким чином u 1 =3; u 3 =0; u 2 =4-3=1;
max : R (u )  2 3  4  2 .
Симплекс-метод є основним і універсальним методом
розв’язку задач ЛП, до якого можна привести любу задачу
ЛП. Алгебраїчною основою симплекс-метода являється
апарат «хорданових виключень», коли вихідна система
обмежень
m
 a ij u j  b i ,  1, n , n  m, b i  0 ,
i
 j 1
приводяться до еквівалентної форми:
m
u   a u  b i ,  1, b , n  0 ,
j0 ij ij b i i
 j 1
де u j0 – опорні, а u jb – вільні змінні.
Для розв’язку задач ЛП її приводять до так званого
канонічного вигляду, для чого обмеження нерівності ___