Page 68 - 4773

5.3. Властивості функцій, неперервних на відрізку

Озн. Якщо функція неперервна в кожній точці інтервалу (a; b),

то вона називається неперервною на цьому інтервалі.

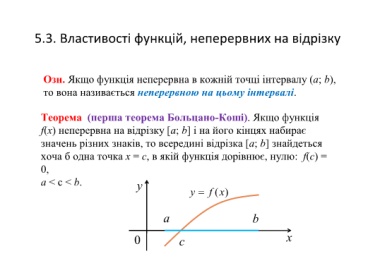
Теорема (перша теорема Больцано-Коші). Якщо функція

f(х) неперервна на відрізку [a; b] і на його кінцях набирає

значень різних знаків, то всередині відрізка [a; b] знайдеться

хоча б одна точка х = с, в якій функція дорівнює, нулю: f(с) =

0,

a < с < b. y

y  ( f ) x

a b

0 c x