Page 14 - 4624

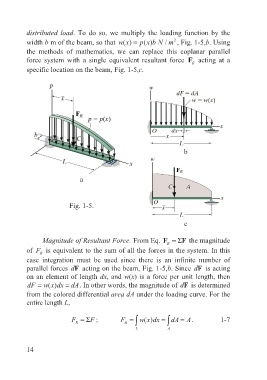
distributed load. To do so, we multiply the loading function by the
2
width b m of the beam, so that ()w x = p ()x bN m , Fig. 1-5,b. Using
/
the methods of mathematics, we can replace this coplanar parallel
force system with a single equivalent resultant force F acting at a
R
specific location on the beam, Fig. 1-5,c.

b

a

Fig. 1-5.

c

Magnitude of Resultant Force. From Eq. F R =ΣF the magnitude
of F is equivalent to the sum of all the forces in the system. In this
R
case integration must be used since there is an infinite number of
parallel forces dF acting on the beam, Fig. 1-5,b. Since dF is acting
on an element of length dx, and w(x) is a force per unit length, then
dF = w ()x dx = dA. In other words, the magnitude of dF is determined
from the colored differential area dA under the loading curve. For the
entire length L,

R ∫
F =Σ ; F = w ()x dx = ∫ dA = A. 1-7
F
R
L A

14