Page 12 - 4624

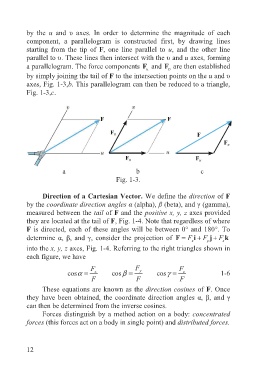
by the u and υ axes. In order to determine the magnitude of each
component, a parallelogram is constructed first, by drawing lines
starting from the tip of F, one line parallel to u, and the other line
parallel to υ. These lines then intersect with the υ and u axes, forming
a parallelogram. The force components F and F are then established
υ
u
by simply joining the tail of F to the intersection points on the u and υ
axes, Fig. 1-3,b. This parallelogram can then be reduced to a triangle,
Fig. 1-3,c.

a b c
Fig. 1-3.

Direction of a Cartesian Vector. We define the direction of F
by the coordinate direction angles α (alpha), β (beta), and γ (gamma),
measured between the tail of F and the positive x, y, z axes provided
they are located at the tail of F, Fig. 1-4. Note that regardless of where
F is directed, each of these angles will be between 0° and 180°. To
determine α, β, and γ, consider the projection of F = F +i F +j F k
z
y
x
into the x, y, z axes, Fig. 1-4. Referring to the right triangles shown in
each figure, we have
F F F
cosα = x cosβ = y cosγ = z 1-6
F F F
These equations are known as the direction cosines of F. Once
they have been obtained, the coordinate direction angles α, β, and γ
can then be determined from the inverse cosines.
Forces distinguish by a method action on a body: concentrated
forces (this forces act on a body in single point) and distributed forces.

12