Page 24 - 4234

The received hypotenuse will be full size of a piece of straight line АВ, and the corner α will
be a natural corner of an inclination of the given piece to a horizontal plane of projections.
Without a finding natural are long a piece it is impossible to find a corner of an inclination of
a straight line to a plane of projections. Therefore if it is required to find corners of an inclination of
a straight line to all planes of projections (П 1, П 2, П 3) it is necessary to define natural length of a
piece on all planes of projections (Fig. 3.15).

Figure 3.15

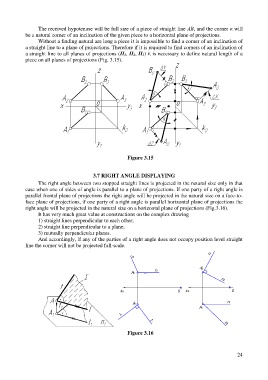
3.7 RIGHT ANGLE DISPLAYING
The right angle between two stopped straight lines is projected in the natural size only in that
case when one of sides of angle is parallel to a plane of projections. If one party of a right angle is
parallel frontal plane of projections the right angle will be projected in the natural size on a face-to-
face plane of projections, if one party of a right angle is parallel horizontal plane of projections the
right angle will be projected in the natural size on a horizontal plane of projections (Fig.3.16).
It has very much great value at constructions on the complex drawing
1) straight lines perpendicular to each other;
2) straight line perpendicular to a plane;
3) mutually perpendicular planes.
And accordingly, if any of the parties of a right angle does not occupy position level straight
line the corner will not be projected full-scale.

n 2
l2

A2
t2
A2
m 2
0 0
x12 x12
n1
A1
A1
l1 t1 m 1

Figure 3.16

24