Page 102 - 4167

  E   . (8.6)

The coefficient E in the last formula is called Young's modulus
Young’s modulus, numerical constant, named after the 18th-century

English physician and physicist Thomas Young, that described the
elastic properties of a solid body undergoing tension or compression in
only one direction, as in the case of a metal rod that after being stretched

or compressed lengthwise returns to its original length. Young’s
modulus is a measure of the ability of a material to withstand changes in
length when under lengthwise tension or compression. Sometimes
referred to as the modulus of elasticity, Young’s modulus is equal to the

longitudinal stress divided by the strain
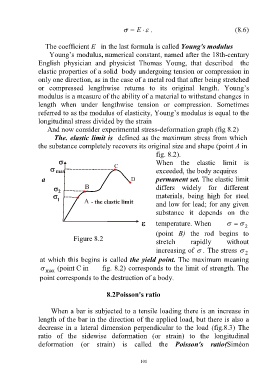
And now consider experimental stress-deformation graph (fig 8.2)
The. elastic limit is defined as the maximum stress from which

the substance completely recovers its original size and shape (point A in
fig. 8.2).
When the elastic limit is

exceeded, the body acquires
a permanent set. The elastic limit
differs widely for different

materials, being high for steel
and low for lead; for any given
substance it depends on the

temperature. When   
2
(point B) the rod begins to
Figure 8.2
stretch rapidly without

increasing of  . The stress 
2
at which this begins is called the yield point. The maximum meaning

 max (point С in fig. 8.2) corresponds to the limit of strength. The
point corresponds to the destruction of a body.

8.2Poisson's ratio

When a bar is subjected to a tensile loading there is an increase in

length of the bar in the direction of the applied load, but there is also a
decrease in a lateral dimension perpendicular to the load (fig.8.3) The
ratio of the sidewise deformation (or strain) to the longitudinal

deformation (or strain) is called the Poisson's ratio(Siméon

101