Page 59 - 35

використанні подвійної логарифмічної системи координат, коли у декартових
координатах по осях відкладають не самі величини, а їх логарифми.

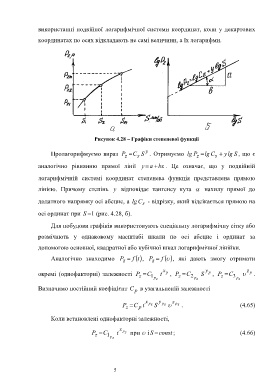
Рисунок 4.28 – Графіки степеневої функції

y
Пролагорифмуємо вираз P  C s S . Отримуємо lg P  lg C  y lg S , що є
z
z
s
аналогічно рівнянню прямої лінії y  a  bx . Це означає, що у подвійній

логарифмічній системі координат степенева функція представлена прямою

лінією. Причому степінь y відповідає тангенсу кута  нахилу прямої до

додатного напрямку осі абсцис, а lg C - відрізку, який відсікається прямою на
s
осі ординат при S 1 (рис. 4.28, б).

Для побудови графіків використовують спеціальну логарифмічну сітку або

розмічають у однаковому масштабі шкали по осі абсцис і ординат за

допомогою основної, квадратної або кубічної шкал логарифмічної лінійки.

Аналогічно знаходимо P  f  t , P  f   , які дають змогу отримати
z
z
x y z
окремі (однофакторні) залежності P  C 1 p z t p , P  C 2 p z S p , P  C 3 p z  p .
z
z
z
Визначимо постійний коефіцієнт C в узагальненій залежності
p

x y z
P  C p t p z S p z  p z . (4.65)
z

Коли встановлені однофакторні залежності,

x
P  C 1 p z t p z при i S  const ; (4.66)
z

5