Page 22 - 35

Середній коефіцієнт тертя  є складною функцією умов різання і ні в

якому разі його не можна ототожнювати з коефіцієнтом тертя в звичайному

розумінні. Найбільш правильно його розглядати як деяку інтегральну

характеристику напруженого стану в зоні контакту стружки з інструментом.

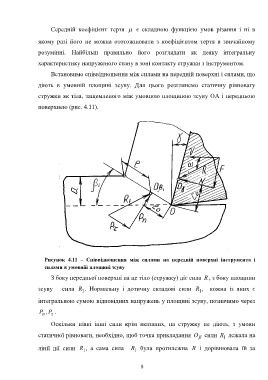
Встановимо співвідношення між силами на передній поверхні і силами, що

діють в умовній площині зсуву. Для цього розглянемо статичну рівновагу

стружки як тіла, защемленого між умовною площиною зсуву ОА і передньою

поверхнею (рис. 4.11).

Рисунок 4.11 – Співвідношення між силами на передній поверхні інструмента і

силами в умовній площині зсуву
З боку передньої поверхні на це тіло (стружку) діє сила R , з боку площини

зсуву – сила R . Нормальну і дотичну складові сили R , кожна із яких є
1
1
інтегральною сумою відповідних напружень у площині зсуву, позначимо через

P n P ,  .

Оскільки ніякі інші сили крім вказаних, на стружку не діють, з умови

статичної рівноваги, необхідно, щоб точка прикладання O сили R лежала на

1
лінії дії сили R , а сама сила R була протилежна R і дорівнювала їй за
1
1

8