Page 188 - 14

191

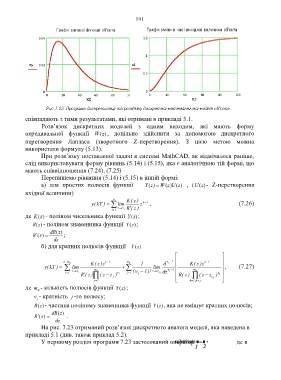
співпадають з тими результатами, які отримані в прикладі 5.1.
Розв’язок дискретних моделей з одним виходом, які мають форму
передавальної функції W (z ) , доцільно здійснити за допомогою дискретного
перетворення Лапласа (зворотного Z-перетворення). З цією метою можна
використати формулу (5.13).
При розв’язку поставленої задачі в системі MathCAD, як відмічалося раніше,
слід використовувати форму рівнянь (5.14) і (5.15), яка є аналогічною тій формі, що
мають співвідношення (7.24), (7.25)
Перепишемо рівняння (5.14) і (5.15) в іншій формі:
а) для простих полюсів функції Y (z ) W (z )U (z ) , ( (zU )- Z-перетворення
вхідної величини)
n K ) z (
( y kT )   lim z k 1 , (7.26)
i
i 1 z z R  z( )
де (zK ) - поліном чисельника функції (zY );
(zR )- поліном знаменника функції (zY );
dR( z)
R (  z)  ;
dz
б) для кратних полюсів функції (zY )
 
 
n m k 1 m v j 1 k 1 
S K z ) z ( S 1 d K z ) z (
( y kT )   lim m   lim j v 1  m  , (7.27)
i 1 z  i z s j v j 1 v( j  )!1 z  v z j dz  s k v 
R  z( )  z (  z j )  ) z ( R  z (  z k v ) 
j 1  k  k,1  j 
де m - кількість полюсів функції (zY );
S
v - кратність j -го полюсу;
j
(zR )- частина поліному знаменника функції (zY ), яка не вміщує кратних полюсів;
dR( z)
R (  z)  .
dz
На рис. 7.23 отриманий розв’язок дискретного аналога моделі, яка наведена в
прикладі 5.1 (див. також приклад 5.2).
У першому розділі програми 7.23 застосований оператор де в