Page 13 - 6686

2 Elements of the theory of dimensions of physical quantities

Dimension - symbolic (lettering) defining of the value,
which reflects its connection with the basic values of the system
and it is the product of these quantities. If physical quantity
does not depend on any of the basic quantities, it is called a
dimensionless (constant quantites are equal to zero, and its
dimension is equal to one). Basic units of international system
(IS) are presented in Table 2.1 [3].
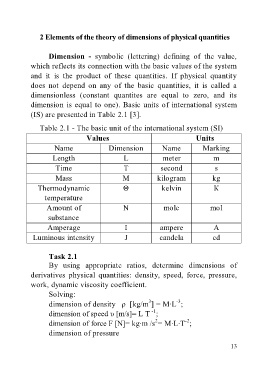
Table 2.1 - The basic unit of the international system (SI)
Values Units
Name Dimension Name Marking
Length L meter m
Time T second s
Mass M kilogram kg
Thermodynamic Θ kelvin К
temperature
Amount of N mole mol
substance
Amperage I ampere A
Luminous intensity J candela cd

Task 2.1
By using appropriate ratios, determine dimensions of
derivatives physical quantities: density, speed, force, pressure,
work, dynamic viscosity coefficient.
Solving:
-3
3
dimension of density ρ [kg/m ] = М∙L ;
-1
dimension of speed υ [m/s]= L T ;
2
-2
dimension of force F [N]= kg∙m /s = М∙L∙T ;
dimension of pressure
13