Page 30 - 6028

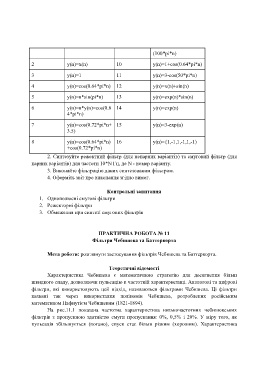
(100*pi*n)

2 y(n)=x(n) 10 y(n)=1+cos(0.64*pi*n)

3 y(n)=1 11 y(n)=3-cos(50*pi*n)

4 y(n)=cos(0.64*pi*n) 12 y(n)=x(n)+sin(n)

5 y(n)=n*sin(pi*n) 13 y(n)=exp(n)*sin(n)

6 y(n)=n*y(n)=cos(0.6 14 y(n)=exp(n)
4*pi*n)

7 y(n)=cos(0.72*pi*n+ 15 y(n)=3-exp(n)
3.5)

8 y(n)=cos(0.64*pi*n) 16 y(n)={1,-1,1,-1,1,-1)
+cos(0.72*pi*n)

2. Синтезуйте режектний фільтр (для непарних варіантів) та смуговий фільтр (для
парних варіантів) для частоти 10*N Гц, де N - номер варіанту.
3. Виконайте фільтрацію даних синтезованим фільтром.
4. Оформіть звіт про виконання згідно вимог.

Контрольні запитання
1. Однополюсні смугові фільтри
2. Режекторні фільтри
3. Обмеження при синтезі смугових фільтрів

ПРАКТИЧНА РОБОТА № 11
Фільтри Чебишева та Баттерворта

Мета роботи: розглянути застосування фільтрів Чебишева та Баттерворта.

Теоретичні відомості
Характеристика Чебишева є математичною стратегію для досягнення більш
швидкого спаду, дозволяючи пульсацію в частотній характеристиці. Аналогові та цифрові
фільтри, які використовують цей підхід, називаються фільтрами Чебишева. Ці фільтри
названі так через використання поліномів Чебишева, розроблених російським
математиком Пафнутієм Чебишевим (1821-1894).
На рис.11.1 показана частотна характеристика низькочастотних чебишовських
фільтрів з пропускною здатністю смуги пропускання: 0%, 0,5% і 20%. У міру того, як
пульсація збільшується (погано), спуск стає більш різким (хорошим). Характеристика