Page 14 - 4906

1.2 Зображення геометричних елементів в ортогональних проекціях
(елементи нарисної геометрії)

До геометричних елементів відносяться:
• точка — нескінченно мала величина, що немає розміру;
• лінія — послідовність незліченної множини точок;
• поверхня — сукупність множини точок, що не мають товщини.
Побудова проекцій геометричних елементів ґрунтується на методі ортогонального
паралельного проектування. В ортогональному проектуванні знаходять кілька проекцій
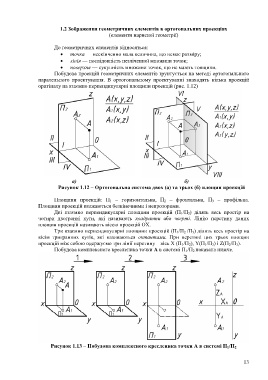
оригіналу на взаємно перпендикулярні площини проекцій (рис. 1.12)

а) б)
Рисунок 1.12 – Ортогональна система двох (a) та трьох (б) площин проекцій

Площини проекцій: П 1 – горизонтальна, П 2 – фронтальна, П 3 – профільна.
Площини проекцій вважаються безкінечними і непрозорими.
Дві взаємно перпендикулярні площини проекцій (П 1/П 2) ділять весь простір на
чотири двогранні кути, які називають квадранти або чверті. Лінію перетину даних
площин проекцій називають віссю проекцій ОХ.
Три взаємно перпендикулярні площини проекцій (П 1/П 2 /П 3) ділять весь простір на
вісім тригранних кутів, які називаються октантами. При перетині цих трьох площин
проекцій між собою одержуємо три лінії перетину – вісь X (П 1/П 2), Y(П 1/П 3) і Z(П 2/П 3).
Побудова комплексного кресленика точки А в системі П 1/П 2 показана нижче.

Рисунок 1.13 – Побудова комплексного кресленика точки А в системі П 1/П 2

13