Page 30 - 4848

y=sim(net,P)  функція моделювання нейронної мережі і збереження
її результатів у масив y, де
net  об’єкт нейронної мережі;
P  вектор вхідних значень.
[m,b,r]=postreg(y(1,:),T(1,:))  функція регресійного аналізу.
Обчислюється лінійна регресія між виходом мережі і правильними
значеннями для того, щоб перевірити якість навчання мережі.

4.3 Виконання роботи
4.3.1 Завдання

Створити однонаправлену нейронну мережу, параметри якої
вибираються студентом за номером варіанту, даного викладачем.

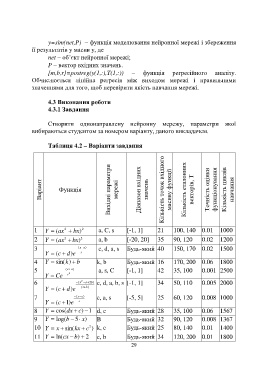
Таблиця 4.2 – Варіанти завдання

Варіант Функція Вихідні параметри мережі Діапазон вхідних значень Кількість точок вхідного масиву функції Кількість еталонних векторів, T Точність оцінки функціонування Кількість циклів навчання

1 Y  (ax  bx ) a, C, s [-1, 1] 21 100, 140 0.01 1000
2
2
2 Y  (ax  bx ) a, b [-20, 20] 35 90, 120 0.02 1200
2
2
3  x (  a) c, d, a, s Будь-який 40 150, 170 0.02 1500
Y  c (  d e ) s
4 Y  sin( k  b k, b Будь-який 16 170, 200 0.06 1800
)
5  (x ) a a, s, C [-1, 1] 42 35, 100 0.001 2500
Y  Ce s 2
6  (x  a 2b ) c, d, a, b, s [-1, 1] 34 50, 110 0.005 2000
2
Y  (c  d )e (s ) b
7  x (  a) c, a, s [-5, 5] 25 60, 120 0.008 1000
Y  c (  e ) 1 s

8 Y  cos(dx  c )  1 d, c Будь-який 28 35, 100 0.06 1567
9 Y  log(b  5 ) x  B Будь-який 32 90, 120 0.008 1367

10 Y  x  sin(kx  c 2 ) k, c Будь-який 25 80, 140 0.01 1400
11 Y  ln(cx  b )  2 c, b Будь-який 34 120, 200 0.01 1800

29