Page 36 - 4660

Discrete random variables

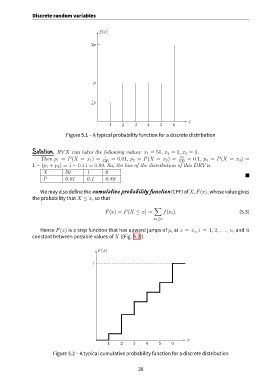
f(x)

2p

p

1 p
2

x
1 2 3 4 5 6

Figure 5.1 – A typical probability function for a discrete distribution

Solution. RV X can takes the following values: x 1 = 50, x 2 = 1, x 3 = 0.
Then p 1 = P(X = x 1 ) = 1 = 0.01, p 2 = P(X = x 2 ) = 10 = 0.1, p 3 = P(X = x 3 ) =
100 100
1 − (p 1 + p 2 ) = 1 − 0.11 = 0.89. So, the law of the distribution of this DRV is
X 50 1 0
P 0.01 0.1 0.89

We may also define thecumulative probability function (CPF) of X, F(x), whose value gives
the probability that X ≤ x, so that

∑
F(x) = P(X ≤ x) = f(x i ). (5.3)
x i ≤x

Hence F(x) is a step function that has upward jumps of p i at x = x i , i = 1, 2, . . . , n, and is
constant between possible values of X ((Fig. 5.2)).

F(x)

1

x
1 2 3 4 5 6
Figure 5.2 – A typical cumulative probability function for a discrete distribution

36