Page 58 - 4617

РУХ ПІД ДІЄЮ ВІДНОВЛЮВАЛЬНОЇ СИЛИ І СИЛИ ОПОРУ

Розділ 2. Рух під дією відновлювальної сили
і сили лінійно-в’язкого опору

Сила лінійно-в’язкого опору – сила опору, пропорційна пер-
шому степеню швидкості: R   v .

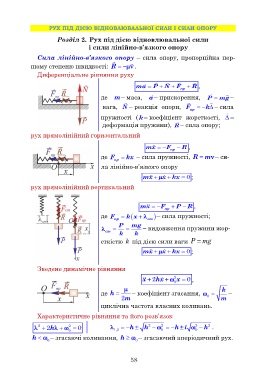
Диференціальне рівняння руху

 ma  P  N пр  F R ,

де m– маса, a– прискорення, P  mg –
вага, N – реакція опори, F пр  k – сила

пружності (k– коефіцієнт жорсткості,  –
деформація пружини), R– сила опору;

рух прямолінійний горизонтальний

mx   F пр  R ,
v
де F пр  kx – сила пружності, R  m – си-
ла лінійно-в’язкого опору
 mx   x kx 0 ;

рух прямолінійний вертикальний

mx   F пр  P  R ,

де F пр  kx ст  – сила пружності;
  
P mg
 ст  k  k – видовження пружини жор-


сткістю k під дією сили ваги P mg
 mx   x kx 0 ;

Зведене динамічне рівняння

x  2hx  2 x  0 ,
0
де h   – коефіцієнт згасання,   k –
0
2m m
циклічна частота власних коливань.

Характеристичне рівняння та його розв’язок

2
2    2h 2   0   h h 2   2  hi  2  h .
0 1,2 0 0
h   – згасаючі коливання, h   – згасаючий аперіодичний рух.
0 0

58