Page 91 - 4560

The general solution of the equation

 Ay sin  t  . (7.34)
0

The equation of harmonic vibrational motion is known. Thus, the
free vibrations of goods Q , that are influenced by the elastic
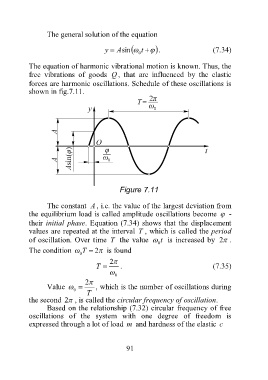
forces are harmonic oscillations. Schedule of these oscillations is
shown in fig.7.11.

Figure 7.11

The constant A , i.e. the value of the largest deviation from
the equilibrium load is called amplitude oscillations become  -
their initial phase. Equation (7.34) shows that the displacement
values are repeated at the interval T , which is called the period
t
of oscillation. Over time T the value  is increased by 2 .
0
The condition  T  2  is found
0
2
T  . (7.35)

0
2 
Value   , which is the number of oscillations during
0
T
the second 2 , is called the circular frequency of oscillation.
Based on the relationship (7.32) circular frequency of free
oscillations of the system with one degree of freedom is
expressed through a lot of load m and hardness of the elastic c

91