Page 23 - 4524

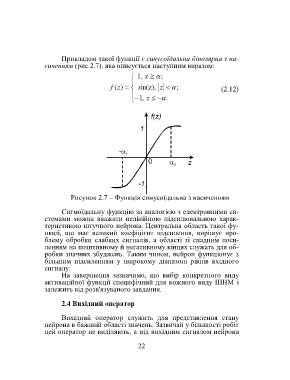
Прикладом такої функції є синусоїдальна біполярна з на-
сиченням (рис.2.7), яка описується наступним виразом:
 ,1 z  ;

f (z )   in(z), zs  ; (2.12)
  ,1 z   .


Рисунок 2.7 – Функція синусоїдальна з насиченням

Сигмоїдальну функцію за аналогією з електронними си-
стемами можна вважати нелінійною підсилювальною харак-
теристикою штучного нейрона. Центральна область такої фу-
нкції, що має великий коефіцієнт підсилення, вирішує про-
блему обробки слабких сигналів, а області зі спадним поси-
ленням на позитивному й негативному кінцях служать для об-
робки значних збуджень. Таким чином, нейрон функціонує з
більшим підсиленням у широкому діапазоні рівнів вхідного
сигналу.
На завершення зазначимо, що вибір конкретного виду
активаційної функції специфічний для кожного виду ШНМ і
залежить від розв'язуваного завдання.

2.4 Вихідний оператор

Вихідний оператор служить для представлення стану
нейрона в бажаній області значень. Зазвичай у більшості робіт
цей оператор не виділяють, а під вихідним сигналом нейрона

22