Page 102 - 4204

ЛЕКЦІЯ 7. ЕЛЕМЕНТИ ОБЧИСЛЮВАЛЬНОЇ ГЕОМЕТРІЇ.

нумерувати у протилежному напрямку. Отже, у будь-якому випа-

дку площа многокутника рівна

1 n
S   x(  x )  y(  y ) .
2 i 1 i i 1 i
i 1

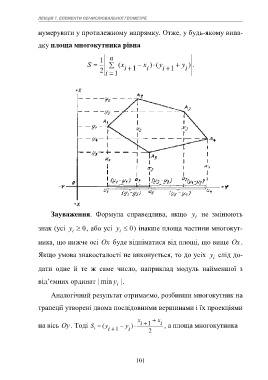
Зауваження. Формула справедлива, якщо y не змінюють
i
знак (усі y i  0, або усі y i  0) інакше площа частини многокут-

ника, що нижче осі Ox буде відніматися від площі, що вище Ox.

Якщо умова знакосталості не виконується, то до усіх y слід до-
i

дати одне й те ж саме число, наприклад модуль найменшої з

від’ємних ординат min| y i |.

Аналогічний результат отримаємо, розбивши многокутник на

трапеції утворені двома послідовними вершинами і їх проекціями

x  x
на вісь Oy. Тоді S  (y i  1  y i )  i  1 i , а площа многокутника
i
2

101