Page 41 - 363_

42

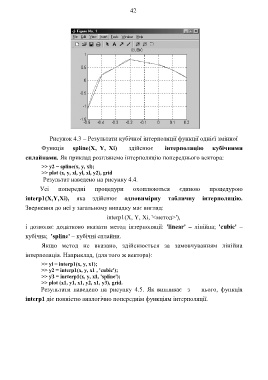
Рисунок 4.3 – Результати кубічної інтерполяції функції однієї змінної
Функція spline(X, Y, Xi) здійснює інтерполяцію кубічними

сплайнами. Як приклад розглянемо інтерполяцію попереднього вектора:

>> y2 = spline(x, y, xl);
>> plot (x, y, xl, yl, xl, y2), grid
Результат наведено на рисунку 4.4.

Усі попередні процедури охоплюються єдиною процедурою
interp1(X,Y,Xi), яка здійснює одновимірну табличну інтерполяцію.

Звернення до неї у загальному випадку має вигляд:

interp1(X, Y, Xi, '<метод>'),
і дозволяє додатково вказати метод інтерполяції: 'linear' – лінійна; 'cubic' –

кубічна; 'spline' – кубічні сплайни.
Якщо метод не вказано, здійснюється за замовчуванням лінійна

інтерполяція. Наприклад, (для того ж вектора):

>> yl = interp1(x, y, x1);
>> y2 = interp1(x, y, x1 , 'cubic');
>> уЗ = inrterp1(x, y, x1, 'spline');
>> plot (x1, y1, x1, y2, x1, y3), grid.
Результати наведено на рисунку 4.5. Як випливає з нього, функція
interp1 діє повністю аналогічно попереднім функціям інтерполяції.