Page 7 - 6760

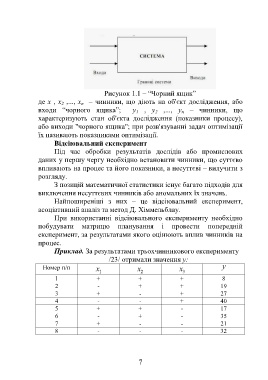
Рисунок 1.1 – “Чорний ящик”
де x , x ,..., x – чинники, що діють на об'єкт дослідження, або
n
2
входи “чорного ящика”; y , y ,..., y – чинники, що
n
2
1
характеризують стан об'єкта дослідження (показники процесу),
або виходи "чорного ящика"; при розв'язуванні задач оптимізації
їх називають показниками оптимізації.
Відсіювальний експеримент
Під час обробки результатів дослідів або промислових

даних у першу чергу необхідно встановити чинники, що суттєво
впливають на процес та його показники, а несуттєві – вилучити з
розгляду.
З позицій математичної статистики існує багато підходів для

виключення несуттєвих чинників або аномальних їх значень.
Найпоширеніші з них – це відсіювальний експеримент,
асоціативний аналіз та метод Д. Хіммельблау.

При використанні відсіювального експерименту необхідно
побудувати матрицю планування і провести попередній
експеримент, за результатами якого оцінюють вплив чинників на
процес.

Приклад. За результатами трьохчинникового експерименту
/23/ отримали значення у:

Номер п/п x x x y
1 2 3
1 + + + 8

2 - + + 19
3 + - + 27
4 - - + 40
5 + + - 17
6 - + - 35
7 + - - 21
8 - - - 32

7