Page 7 - 6416

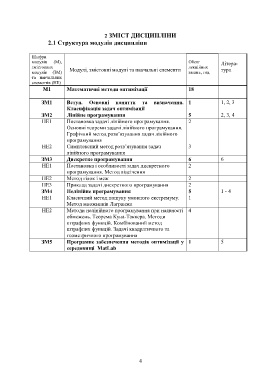
2 ЗМІСТ ДИСЦИПЛІНИ
2.1 Структура модулів дисципліни

Шифри
модулів (М), Обсяг Літера-
змістовних Модулі, змістовні модулі та навчальні елементи лекційних тура
модулів (ЗМ) занять, год.
та навчальних
елементів (НЕ)
М1 Математичні методи оптимізації 18

ЗМ1 Вступ. Основні поняття та визначення. 1 1, 2, 3
Класифікація задач оптимізації
ЗМ2 Лінійне програмування 5 2, 3, 4
НЕ1 Постановка задачі лінійного програмування. 2
Основні теореми задачі лінійного програмування.
Графічний метод розв’язування задач лінійного
програмування
НЕ2 Симплексний метод розв’язування задач 3
лінійного програмування
ЗМ3 Дискретне програмування 6 6
НЕ1 Постановка і особливості задач дискретного 2
програмування. Метод відсічення
НЕ2 Метод гілок і меж 2
НЕ3 Приклад задачі дискретного програмування 2
ЗМ4 Нелінійне програмування 5 1 - 4
НЕ1 Класичний метод пошуку умовного екстремуму. 1
Метод множників Лагранжа
НЕ2 Методи нелінійного програмування при наявності 4
обмежень. Теорема Куна-Таккера. Методи
штрафних функцій. Комбінований метод
штрафних функцій. Задачі квадратичного та
геометричного програмування
ЗМ5 Програмне забезпечення методів оптимізації у 1 5
середовищі MatLab

4