Page 46 - 6217

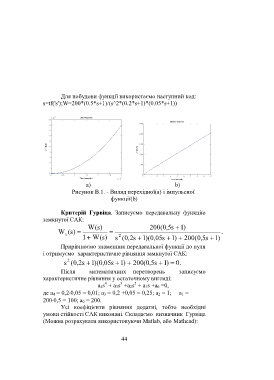
Для побудови функції використаємо наступний код:
s=tf('s');W=200*(0.5*s+1)/(s^2*(0.2*s+1)*(0.05*s+1))

а) b)
Рисунок В.1. - Виляд перехідної(а) і імпульсної
функції(b)

Критерій Гурвіца. Записуємо передавальну функцію
замкнутої САК:
W ) s ( 200 s 5 , 0 (  ) 1
W з ) s (   .
1 W ) s ( s 2 s 2 , 0 (  1 )( , 0 05 s  ) 1  200 s 5 , 0 (  ) 1

Прирівнюємо знаменник передавальної функції до нуля
і отримуємо характеристичне рівняння замкнутої САК:

s 2 s 2 , 0 (  1 )( , 0 05 s  ) 1  200 s 5 , 0 (  ) 1  . 0
Після математичних перетворень записуємо
характеристичне рівняння у остаточному вигляді:
4
2
3
a 4s + a 3s +a 2s + a 1s +a 0 =0,
де a 4 = 0,20,05 = 0,01; a 3 = 0,2 +0,05 = 0,25; a 2 = 1; a 1 =
2000,5 = 100; a 0 = 200.
Усі коефіцієнти рівняння додатні, тобто необхідні
умови стійкості САК виконані. Складаємо визначник Гурвіца
(Можна розрахувати використовуючи Matlab, або Mathcad):

44