Page 64 - 6099
P. 64
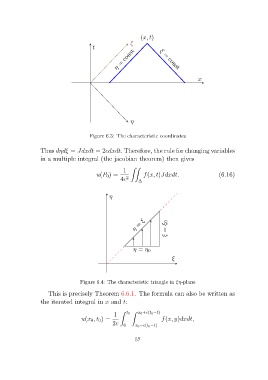
(x, t)
ξ
t ξ
const =
= const
η
x
η
Figure 6.3: The characteristic coordinates
Thus dηdξ = Jdxdt = 2cdxdt. Therefore, the rule for changing variables
in a multiple integral (the jacobian theorem) then gives
ZZ
1
u(P ) = f(x, t)Jdxdt. (6.16)
0
4c 2 ∆
η
ξ
= ξ 0
η =
ξ
η = η 0
ξ
Figure 6.4: The characteristic triangle in ξη-plane
This is precisely Theorem 6.6.1. The formula can also be written as
the iterated integral in x and t:
Z Z x 0 +c(t 0 −t)
1 t 0
u(x , t ) = f(x, y)dxdt,
0
0
2c 0 x 0 −c(t 0 −t)
57