Page 62 - 49

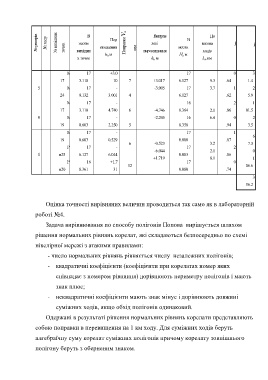
№ реперів № ходу № вихідних точок исоти евищення Поправки ν і , мм лені исоти вжина P P
В
Виправ
До
Пер
В
вихідни
h i, м перевищення Н і, м ходів
х точок h i, м L i, км

М 17 +3.0 + 17 0 3
17 3.110 10 7 +3.017 6.127 9.3 .64 1.4
5 М 17 - - -3.005 17 3.7 1 2
24 9.132 3.001 4 6.127 .62 5.9
М 17 - - 16 2 1
17 3.110 4.740 6 -4.746 8.364 2.1 .86 01.5
0 М 17 - + -2.245 16 6.4 0 2
19 0.603 2.250 5 8.358 .94 3.5
М 17 - 17 1
+ 6
19 0.603 0.529 0.080 .87
6 -0.523 3.2 7.3
Р 17 - 17 2
0 -6.044 2.1 0
1 п25 6.127 6.044 0.083 .86
- +1.719 8.1 1
Р 16 +1.7 17 0
12 06.6
п20 8.361 31 0.080 .74

3

56.2

Оцінка точності вирівняних величин проводиться так само як в лабораторній

роботі №4.

Задача вирівнювання по способу полігонів Попова вирішується шляхом
рішення нормальних рівнянь корелат, які складаються безпосередньо по схемі

нівелірної мережі з атакими правилами:

- число нормальних рівнянь рівняється числу незалежних полігонів;

- квадратичні коефіцієнти (коефіцієнти при корелатах номер яких

співпадає з номером рівняння) дорівнюють периметру полігонів і мають

знак плюс;

- неквадратичні коефіцієнти мають знак мінус і дорівнюють довжині
суміжних ходів, якщо обхід полігонів одинаковий.

Одержані в результаті рішення нормальних рівнянь корелати представляють

собою поправки в перевищення на 1 км ходу. Для суміжних ходів беруть

алгебраїчну суму корелат суміжних полігонів причому корелату зовнішнього

полігону беруть з оберненим знаком.