Page 123 - 4749

h J
1  2 . (6.27)
h J
2 1
Substituting in (6.27) values J  t b 3 12 and J  t b 3 12 and
1 1 1 2 2 2
considering that h  h  , we obtain expressions for the
h
1 2
distances h and h :
1 2

3
hJ t b h
h  2  2 2 , (6.28)
1 3 3
J  J t b  t b
1 2 1 1 2 2
3
hJ t b h
h  1  1 1 . (6.29)
2 3 3
J  J t b  t b
1 2 1 1 2 2
t
In the particular case when t  and b  b (symmetric
1 2 1 2
double-T profile), i.e. the axis y is the axis of symmetry from the
formulas (6.28) and (6.29), we obtain:
h  h  h 2 ,
1 2
i.e., the bending center coincides with the center of gravity.

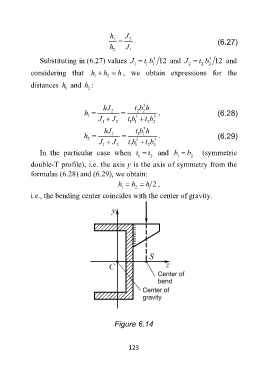
Figure 6.14

123