Page 152 - 4679

Z

2

2

1

1

0
Х

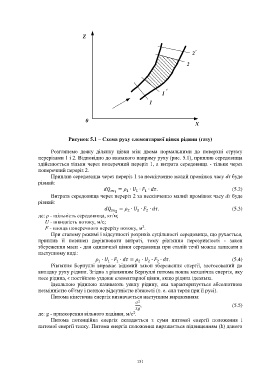
Рисунок 5.1 – Схема руху елементарної цівки рідини (газу)

Розглянемо деяку ділянку цівки між двома нормальними до поверхні струму
перерізами 1 і 2. Відповідно до вказаного напряму руху (рис. 5.1), приплив середовища
здійснюється тільки через поперечний переріз 1, а витрата середовища - тільки через
поперечний переріз 2.
Приплив середовища через переріз 1 за нескінченно малий проміжок часу dτ буде
рівний:
1 = ∙ ∙ ∙ . (5.2)
1
1
1
Витрата середовища через переріз 2 за нескінченно малий проміжок часу dτ буде
рівний:
2 = ∙ ∙ ∙ . (5.3)
2
2
2
де: ρ - щільність середовища, кг/м;
U - швидкість потоку, м/с;
2
F - площа поперечного перерізу потоку, м .
При сталому режимі і відсутності розривів суцільності середовища, що рухається,
приплив її повинен дорівнювати витраті, тому рівняння нерозривності - закон
збереження маси - для одиничної цівки середовища при сталій течії можна записати в
наступному виді:
∙ ∙ ∙ = ∙ ∙ ∙ . (5.4)
2
2
2
1
1
1
Рівняння Бернуллі виражає відомий закон збереження енергії, застосований до
випадку руху рідини. Згідно з рівнянням Бернуллі питома повна механічна енергія, яку
несе рідина, є постійною уздовж елементарної цівки, якщо рідина ідеальна.
Ідеальною рідиною називають уявну рідину, яка характеризується абсолютною
незмінністю об'єму і повною відсутністю в'язкості (т. е. сил тертя при її русі).
Питома кінетична енергія визначається наступним вираженням:
2
, (5.5)
2
2
де: g - прискорення вільного падіння, м/с .
Питома потенційна енергія складається з суми питомої енергії положення і
питомої енергії тиску. Питома енергія положення виражається підвищенням (h) даного

151