Page 84 - 4660

Experiments, samples and populations

Table 2.3 – Frequency Distribution for the Compressive Strength Data in Table 2.2

[70;90) [90;110) [110;130) [130;150) [150;170) [170;190) [190;210) [210;230) [230;250)
2 3 6 14 22 17 10 4 2
0.0250 0.0375 0.0760 0.1750 0.2750 0.2125 0.1250 0.0500 0.0250
0.025 0.0625 0.1375 0.3125 0.5875 0.8000 0.9250 0.9750 1.0000

bins, each of width 20 psi, give a reasonable frequency distribution, so the frequency distribution
in Table 2.3 is based on nine bins.
The third row of Table 2.3 contains a relative frequency distribution. The relative
frequencies are found by dividing the observed frequency in each bin by the total number of
observations. The last row of Table 2.3 expresses the relative frequencies on a cumulative basis.
Frequency distributions are often easier to interpret than tables of data. For example, from Table
2.3 it is very easy to see that most of the specimens have compressive strengths between 130 and
190 psi and that 97.5 percent of the specimens fail below 230 psi.
The histogram is a visual display of the frequency distribution. The steps for constructing a
histogram follow.
1. Label the bin (class interval) boundaries on a horizontal scale.
2. Mark and label the vertical scale with the frequencies or the relative frequencies.
3. Above each bin, draw a rectangle where height is equal to the frequency (or relative
frequency) corresponding to that bin.
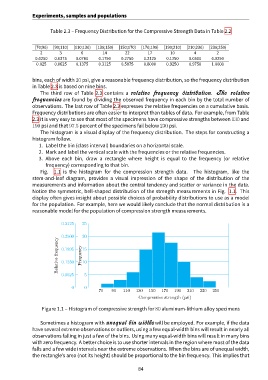
Fig. 1.1 is the histogram for the compression strength data. The histogram, like the
stem-and-leaf diagram, provides a visual impression of the shape of the distribution of the
measurements and information about the central tendency and scatter or variance in the data.
Notice the symmetric, bell-shaped distribution of the strength measurements in Fig. 1.1. This
display often gives insight about possible choices of probability distributions to use as a model
for the population. For example, here we would likely conclude that the normal distribution is a
reasonable model for the population of compression strength measurements.

0.3125 25

0.2500 20
frequency 0.1895 Frequency 15

Relative 0.1250 10

0.0625 5

0 0
70 90 110 130 150 170 190 210 230 250
Compressive strength (psi)

Figure 1.1 – Histogram of compressive strength for 80 aluminum-lithium alloy specimens

Sometimes a histogram with unequal bin widths will be employed. For example, if the data
have several extreme observations or outliers, using a few equal-width bins will result in nearly all
observations falling in just a few of the bins. Using many equal-width bins will result in many bins
with zero frequency. A better choice is to use shorter intervals in the region where most of the data
falls and a few wide intervals near the extreme observations. When the bins are of unequal width,
the rectangle’s area (not its height) should be proportional to the bin frequency. This implies that

84