Page 321 - 4511

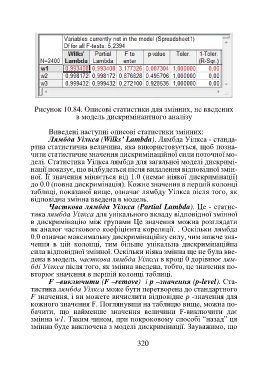
Рисунок 10.84. Описові статистики для змінних, не введених
в модель дискримінантного аналізу

Виведені наступні описові статистики змінних:
Лямбда Уілкса (Wilks’ Lambda). Лямбда Уілкса - станда-
ртна статистична величина, яка використовується, щоб позна-
чити статистичне значення дискримінаційної сили поточної мо-
делі. Статистика Уілкса лямбда для загальної моделі дискримі-
нації показує, що відбудеться після видалення відповідної змін-
ної. Її значення міняється від 1.0 (немає ніякої дискримінації)
до 0.0 (повна дискримінація). Кожне значення в першій колонці
таблиці, показаної вище, означає лямбду Уілкса після того, як
відповідна змінна введена в модель.
Часткова лямбда Уілкса (Partial Lambda). Це - статис-
тика лямбда Уілкса для унікального вкладу відповідної змінної
в дискримінацію між групами Це значення можна розглядати
як аналог часткового коефіцієнта кореляції. . Оскільки лямбда
0.0 означає максимальну дискримінаційну силу, чим нижче зна-
чення в цій колонці, тим більше унікальна дискримінаційна
сила відповідної змінної. Оскільки ніяка змінна ще не була вве-
дена в модель, часткова лямбда Уілкса в кроці 0 дорівнює лям-
бді Уілкса після того, як змінна введена, тобто, це значення по-
вторює значення в першій колонці таблиці.
F –виключити (F –remove) і p –значення (p-level). Ста-
тистика лямбда Уілкса може бути перетворена до стандартного
F значення, і ви можете вичислити відповідне p -значення для
кожного значення F. Поглянувши на таблицю вище, можна по-
бачити, що найменше значення величини F-виключити дає
змінна w1. Таким чином, при покроковому способі “назад” ця
змінна буде виключена з моделі дискримінації. Зауважимо, що

320