Page 94 - 4496

2
2 2

1
1 1

3
5 3 3
5

4

4
4
а б в

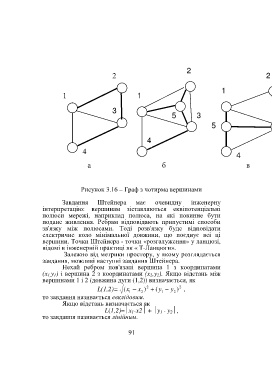
Рисунок 3.16 – Граф з чотирма вершинами

Завдання Штейнера має очевидну інженерну
інтерпретацію: вершинам зіставляються еквіпотенціальні
полюси мережі, наприклад полюса, на які повинне бути
подане живлення. Ребрам відповідають припустимі способи
зв'язку між полюсами. Тоді розв'язку буде відповідати
електричне коло мінімальної довжини, що поєднує всі ці
вершини. Точки Штейнера - точки «розгалуження» у ланцюзі,
відомі в інженерній практиці як « Т-Ланцюги».
Залежно від метрики простору, у якому розглядається
завдання, можливі наступні завдання Штейнера.
Нехай ребром пов'язані вершина 1 з координатами
(x 1,y 1) і вершина 2 з координатами (x 2,y 2). Якщо відстань між
вершинами 1 і 2 (довжина дуги (1,2)) визначається, як
L(1,2)= (x  x 2 )  (y  y 2 ) ,
2
2
1
1
то завдання називається евклідовим.
Якщо відстань визначається як
L(1,2)=x 1-x2 + y 1 - y 2,
то завдання називається лінійним.
91