Page 108 - 4496

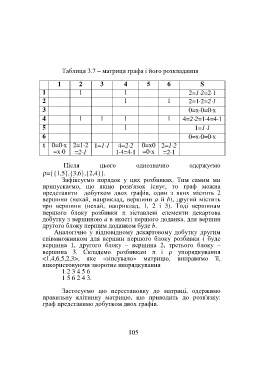
Таблиця 3.7 – матриця графа і його розкладання

1 2 3 4 5 6 S
1 1 1 2=12=21
2 1 1 2=12=21
3 0=х0=0х
4 1 1 1 1 4=22=14=41
5 1 1=11
6 0=х0=0х
t 0=0·х 2=1·2 1=11 4=22 0=х0 2=12
=х·0 =21 1·4=4·1 =0·х =2·1

Після цього однозначно одержуємо
={{1,5},{3,6},{2,4}}.
Зафіксуємо порядок у цих розбивках. Тим самим ми
припускаємо, що якщо розв'язок існує, то граф можна
представити добутком двох графів, один з яких містить 2
вершини (нехай, наприклад, вершини а й b), другий містить
три вершини (нехай, наприклад, 1, 2 і 3). Тоді вершинам
першого блоку розбивки  зіставлені елементи декартова
добутку з вершиною а в якості першого доданка, для вершин
другого блоку першим доданком буде b.
Аналогічно у відповідному декартовому добутку другим
співмножником для вершин першого блоку розбивки ( буде
вершина 1, другого блоку – вершина 2, третього блоку –
вершина 3. Складемо розбивкам  і  упорядкування
<1,4,6,5,2,3>, яке «зіпсувало» матрицю, виправимо її,
використовуючи зворотне впорядкування
1 2 3 4 5 6
1 5 6 2 4 3.

Застосуємо цю перестановку до матриці, одержимо
правильну клітинну матрицю, що приводить до розв'язку:
граф представимо добутком двох графів.

105