Page 7 - 4395

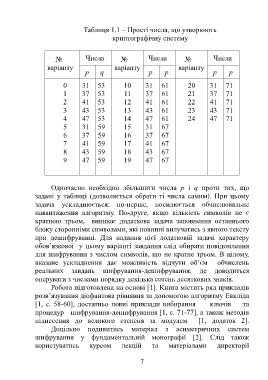
Таблиця 1.1 – Прості числа, що утворюють
криптографічну систему

№ Числа № Числа № Числа
варіанту варіанту варіанту
p q p p p p

0 31 53 10 31 61 20 31 71
1 37 53 11 37 61 21 37 71

2 41 53 12 41 61 22 41 71
3 43 53 13 43 61 23 43 71
4 47 53 14 47 61 24 47 71
5 31 59 15 31 67

6 37 59 16 37 67
7 41 59 17 41 67
8 43 59 18 43 67

9 47 59 19 47 67

Одночасно необхідно збільшити числа p i q проти тих, що

задані у таблиці (дозволяється обрати ті числа самим). При цьому
задача ускладнюється: по-перше, посилюється обчислювальне
навантаження алгоритму. По-друге, якщо кількість символів не є
кратною трьом, виникає додаткова задача заповнення останнього

блоку сторонніми символами, які повинні вилучатись з явного тексту
при дешифруванні. Для надання цієї додатковій задачі характеру
обов’язкової у цьому варіанті завдання слід обирати повідомлення

для шифрування з числом символів, що не кратне трьом. В цілому,
вказане ускладнення дає можливість відчути об’єм обчислень
реальних завдань шифрування-дешифрування, де доводиться
оперувати з числами порядку декілька сотень десяткових знаків.

Робота підготовлена на основі [1]. Книга містить ряд прикладів
розв’язування діофантова рівняння за допомогою алгоритму Евкліда
[1, с. 58-60], достатньо повні приклади вибирання ключів та

процедур шифрування-дешифрування [1, с. 71-77], а також методів
піднесення до великого степеня за модулем [1, додаток 2].
Доцільно подивитись матеріал з асиметричних систем

шифрування у фундаментальній монографії [2]. Слід також
користуватись курсом лекцій та матеріалами директорії

7