Page 28 - 2587

y5=0.7*pulstran(t,d,'gauspuls',1,0.5);
figure(6)
plot(t,y5),grid
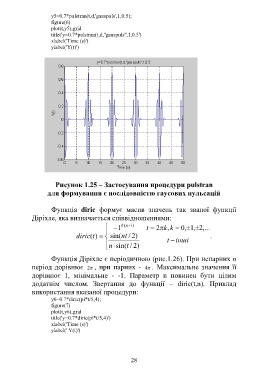
title('y=0.7*pulstran(t,d,''gauspuls'',1,0.5')
xlabel('Time (s)')
ylabel('Y(t)')

Рисунок 1.25 – Застосування процедури pulstran

для формування є послідовністю гаусових пульсацій

Функція diric формує масив значень так званої функції

Діріхле, яка визначається співвідношеннями:
 1 k n (  )1 t  2  kk,  ,0  ,1  ,...2

diric( t)  sin( nt 2/ ) .

  n sin( t 2/ ) t інші


Функція Діріхле є періодичною (рис.1.26). При непарних n
період дорівнює 2 , при парних - 4 . Максимальне значення її

дорівнює 1, мінімальне - -1. Параметр n повинен бути цілим
додатнім числом. Звертання до функції – diric(t,n). Приклад
використання вказаної процедури:
y6=0.7*diric(pi*t/5,4);
figure(7)
plot(t,y6),grid
title('y=0.7*diric(pi*t/5,4)')
xlabel('Time (s)')
ylabel(' Y(t)')

28