Page 44 - 106

43

 
g  0,x 0 ,   f       ln   R      R 
 
   ,  ,
    arctg   R  2 2 2 ;
       ,  ,

 1 1 1
   ,  ,
 2 2 2
 V xz  0,x 0 ,   f   ln   R  ; (2.19)
  1  , 1  , 1
   ,  ,
 V  0,x 0 ,   f   arctg    2 2 2 ;
 zz   R   ,  ,
 1 1 1
 R   2   2   2 ;




де  1   1  x ;  2   2  x .

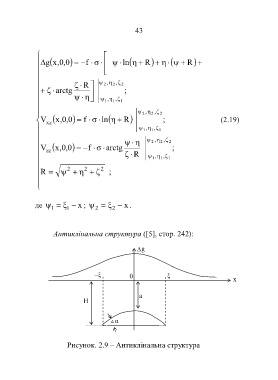
Aнтиклінальна структура ([5], стор. 242):

g

 0 
x

a
H



Рисунок. 2.9 – Aнтиклінальна структура