Page 131 - 6197

і 2 5, , як це відображено на рис 2.20 де показано повне
дерево розгалуження.

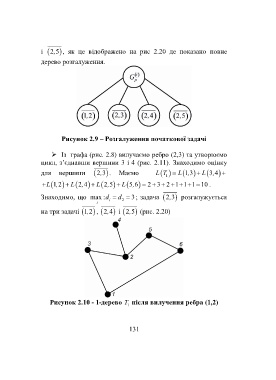
Рисунок 2.9 – Розгалуження початкової задачі

 Із графа (рис. 2.8) вилучаємо ребро (2,3) та утворюємо
цикл, з’єднавши вершини 3 і 4 (рис. 2.11). Знаходимо оцінку
1
для вершини 2 3,  . Маємо L T 1 L   3,  L 3 4,  
  
 L   2,  L 2 4,  L 2 5,  L 5 6,   2 3 2 1 1 1 10      .
1
Знаходимо, що max :d  d  3; задача 2 3,  розгалужується
i i 2
1
на три задачі   2, , 2 4,  і 2 5,  (рис. 2.20)

Рисунок 2.10 - 1-дерево T після вилучення ребра (1,2)
1

131