Page 27 - 4703

видаються мережею, за допомогою матриці втрат (Bishop,
1995). Як правило, краще всього постаратися зробити так, щоб
спостереження різних типів були представлені рівномірно, і
відповідно до цього інтерпретувати результати, які видає ме-
режа.

Як навчається багатошаровий персептрон
Ми зможемо краще зрозуміти, як влаштований і як нав-
чається багатошаровий персептрон (MLP), якщо з'ясуємо, які
функції він здатний моделювати. Згадаємо, що рівнем акти-
вації елементу називається зважена сума його входів з дода-
ним до неї пороговим значенням. Таким чином, рівень акти-
вації є простою лінійною функцією входів. Ця активація потім
перетвориться за допомогою сигмоїдної кривої (що має S -
подібну форму).
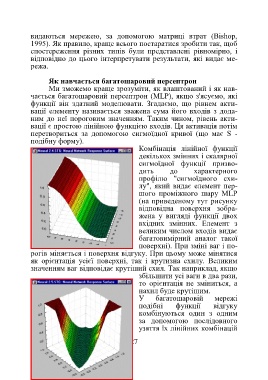
Комбінація лінійної функції
декількох змінних і скалярної
сигмоїдної функції призво-
дить до характерного
профілю "сигмоїдного схи-
лу", який видає елемент пер-
шого проміжного шару MLP
(на приведеному тут рисунку
відповідна поверхня зобра-
жена у вигляді функції двох
вхідних змінних. Елемент з
великим числом входів видає
багатовимірний аналог такої
поверхні). При зміні ваг і по-
рогів міняється і поверхня відгуку. При цьому може мінятися
як орієнтація усієї поверхні, так і крутизна схилу. Великим
значенням ваг відповідає крутіший схил. Так наприклад, якщо
збільшити усі ваги в два рази,
то орієнтація не зміниться, а
нахил буде крутішим.
У багатошаровій мережі
подібні функції відгуку
комбінуються один з одним
за допомогою послідовного
узяття їх лінійних комбінацій

27