Page 38 - 4638

Many applications involving convective heat transfer take place within pipes, tubes,
or some similar cylindrical device. In such circumstances, the surface area of heat

transfer normally given in the convection equation varies as heat passes through the
cylinder. In addition, the temperature difference existing between the inside and the

outside of the pipe, as well as the temperature differences along the pipe, necessitates
the use of some average temperature value in order to analyze the problem. This

average temperature difference is called the log mean temperature difference (LMTD),

described earlier.

For definition of the log mean temperature difference it need use equation

 t  t  s
g
 t  , (3.7)
lm
t 
ln g
t 
s
where t , t – greater and smaller temperature differences between working fluid on
б м

the ends of heat exchanger.

LMTD is the temperature difference at one end of the heat exchanger minus the temperature
difference at the other end of the heat exchanger, divided by the natural logarithm of the ratio of these

two temperature differences. The above definition for LMTD involves two important assumptions: (1)
the fluid specific heats do not vary significantly with temperature, and (2) the convection heat transfer

coefficients are relatively constant throughout the heat exchanger.

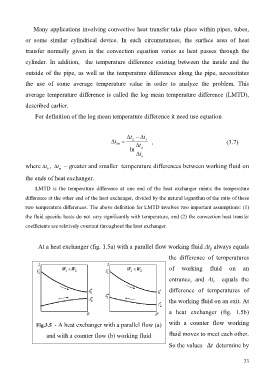
At a heat exchanger (fig. 1.5a) with a parallel flow working fluid Δt g always equals

the difference of temperatures

of working fluid on an

entrance, and Δt s equals the

difference of temperatures of

the working fluid on an exit. At

a heat exchanger (fig. 1.5b)

Fig.3.5 - А heat exchanger with a parallel flow (a) with a counter flow working

fluid moves to meet each other.
and with a counter flow (b) working fluid
So the values t determine by

33