Page 15 - 4625

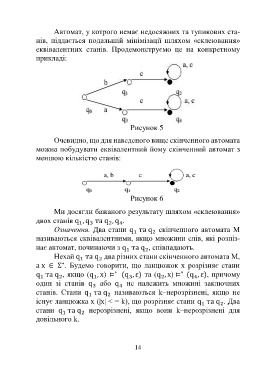
Автомат, у котрого немає недосяжних та тупикових ста-
нів, піддається подальшій мінімізації шляхом «склеювання»
еквівалентних станів. Продемонструємо це на конкретному
прикладі:

Рисунок 5

Очевидно, що для наведеного вище скінченного автомата
можна побудувати еквівалентний йому скінченний автомат з
меншою кількістю станів:

Рисунок 6

Ми досягли бажаного результату шляхом «склеювання»
двох станів q , q та q , q .
3
1
4
2
Означення. Два стани q та q скінченного автомата М
2
1
називаються еквівалентними, якщо множини слів, які розпіз-
нає автомат, починаючи з q та q , співпадають.
1
2
Нехай q та q два різних стани скінченного автомата М,
2
1
∗
a х ∈ Σ . Будемо говорити, що ланцюжок х розрізняє стани
∗
∗
q та q , якщо (q , х) ⊨ (q , ε) та (q , х) ⊨ (q , ε), причому
1
4
2
3
2
1
один зі станів q або q не належить множині заключних
4
3
станів. Стани q та q називаються k–нерозрізнені, якщо не
2
1
існує ланцюжка х (|х| < = k), що розрізняє стани q та q . Два
1
2
стани q та q нерозрізнені, якщо вони k–нерозрізнені для
2
1
довільного k.
14