Page 20 - 4387

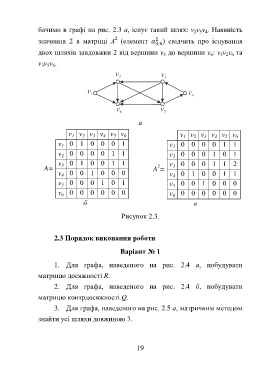
бачимо в графі на рис. 2.3 а, існує такий шлях: v v v . Наявність
2 5 4
2 2
значення 2 в матриці А (елемент ) свідчить про існування
3,6
двох шляхів завдовжки 2 від вершини v до вершини v : v v v та
3
3 2 6
6
v v v .
3 5 6

а

v v v v v v v v v v v v
3
2
1
6
5
4
1
5
6
3
4
2
v 0 1 0 0 0 1 v 0 0 0 0 1 1
1
1
v 0 0 0 0 1 1 v 0 0 0 1 0 1
2
2
v 0 1 0 0 1 1 v 0 0 0 1 1 2
2
A= 3 A = 3
v 0 0 1 0 0 0 v 0 1 0 0 1 1
4
4
v 0 0 0 1 0 1 v 0 0 1 0 0 0
5
5
v 0 0 0 0 0 0 v 0 0 0 0 0 0
6
6
б в

Рисунок 2.3.
2.3 Порядок виконання роботи
Варіант № 1
1. Для графа, наведеного на рис. 2.4 а, побудувати
матрицю досяжності R.

2. Для графа, наведеного на рис. 2.4 б, побудувати

матрицю контрдосяжності Q.

3. Для графа, наведеного на рис. 2.5 а, матричним методом

знайти усі шляхи довжиною 3.

19