Page 18 - 4386

називається прямою сумою графів G і G , якщо множини вершин
2
1
V і V не перетинаються (V ∩V =∅).
2
2
1
1
Перетином і різницею графів G =(V, E ) і G =(V, E ) з
1
2
2
1
однаковими множинами вершин називаються графи –
G´=(V, E ∩E ) та G´´=(V, E \E ) відповідно; позначаються –
1
2
1
2
G´=G ∩G та G´´=G \G .
2
1
2
1
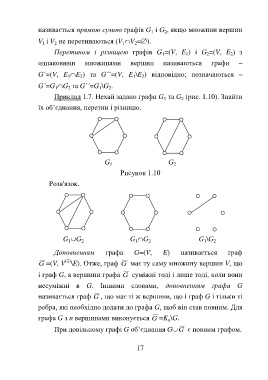
Приклад 1.7. Нехай задано графи G та G (рис. 1.10). Знайти
1
2
їх об’єднання, перетин і різницю.

G 1 G
2
Рисунок 1.10

Розв'язок.

G ∪G 2 G ∩G 2 G \G
1
1
1
2
Доповненням графа G=(V, E) називається граф
(2)
G =(V, V \E). Отже, граф G має ту саму множину вершин V, що

і граф G, а вершини графа G суміжні тоді і лише тоді, коли вони

несуміжні в G. Іншими словами, доповненням графа G

називається граф G , що має ті ж вершини, що і граф G і тільки ті

ребра, які необхідно додати до графа G, щоб він став повним. Для

графа G з n вершинами виконується G =K \G.
n
При довільному графі G об’єднання G∪G є повним графом.

17